260 (number)
260 (two hundred [and] sixty) is the magic constant of the n×n normal magic square and n-queens problem for n = 8, the size of an actual chess board.
| Cardinal | Two hundred [and] sixty |
| Ordinal | 260th |
| Factorization | 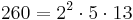 |
| Roman numeral | CCLX |
| Binary | 100000100 |
| Hexadecimal | 104 |
260 is also the magic constant of the Franklin magic square devised by Benjamin Franklin.
| 52 | 61 | 4 | 13 | 20 | 29 | 36 | 45 |
| 14 | 3 | 62 | 51 | 46 | 35 | 30 | 19 |
| 53 | 60 | 5 | 12 | 21 | 28 | 37 | 44 |
| 11 | 6 | 59 | 54 | 43 | 38 | 27 | 22 |
| 55 | 58 | 7 | 10 | 23 | 26 | 39 | 42 |
| 9 | 8 | 57 | 56 | 41 | 40 | 25 | 24 |
| 50 | 63 | 2 | 15 | 18 | 31 | 34 | 47 |
| 16 | 1 | 64 | 49 | 48 | 33 | 32 | 17 |
The minor diagonal gives 260, and in addition a number of combinations of two half diagonals of four numbers from a corner to the center give 260.
260 may also refer to the years AD 260 and 260 BC.
261–269
Two hundred [and] sixty-one 261 = 32·29, nonagonal number, Harshad number, number of possible unfolded tesseract patterns
Two hundred [and] sixty-two 262 = 2·131, meandric number, open meandric number, untouchable number
Two hundred [and] sixty-three 263 prime, safe prime, sum of five consecutive primes (43 + 47 + 53 + 59 + 61), balanced prime, Chen prime, Eisenstein prime with no imaginary part, strictly non-palindromic number
Two hundred [and] sixty-four 264 = 23·3·11, Harshad number
Two hundred [and] sixty-five 265 = 5·53, Padovan number, centered square number, Smith number, subfactorial 6.
Two hundred [and] sixty-six 266 = 2·7·19, sphenic number, Harshad number, nontotient, noncototient, self number, repdigit in base 11 (222). 266 is also the index of the largest proper subgroups of the sporadic group known as the Janko group J1.
Two hundred [and] sixty-seven 267 = 3·89, the number of groups of order 64, see [1].
267: Area code for Pennsylvania, USA (Philadelphia area including its suburbs in eastern Montgomery County and most of Bucks County, overlays with 215)
Two hundred [and] sixty-eight 268 = 22·67, noncototient, untouchable number
Two hundred [and] sixty-nine 269 prime, twin prime with 271, sum of three consecutive primes (83 + 89 + 97), Chen prime, Eisenstein prime with no imaginary part, highly cototient number, strictly non-palindromic number